FEM for discrete data

Here, we describe the version of FEM that requires discrete data, that is variables \(x_i,y\) which take on values from a finite set of symbols. In biology, such data may occur naturally (the DNA sequences that form genes or the amino acid sequences that form proteins, for example) or may result from discretizing continuous variables (assigning neurons’ states to on or off, for example).

Model

The distribution \(p\) that we wish to learn operates on the one-hot encodings of discrete variables defined as follows. Assume the variable \(x_i\) takes on one of \(m_i\) states symbolized by the first \(m_i\) positive integers, i.e. \(x_i\in\{1,2,\ldots,m_i\}\). The one-hot encoding \(\sigma_i\in\{0,1\}^{m_i}\) of \(x_i\) is a vector of length \(m_i\) whose \(j^{th}\), \(j=1,\ldots,m_i\) component is

\[\begin{split}\sigma_{ij}(x_i) = \begin{cases} 1 & \text{ if }x_i=j \\ 0 & \text{otherwise}\end{cases}\end{split}\]

Note that \(\sigma_i\) is a boolean vector with exactly one 1 and the rest 0’s. Assume that we observe \(n\) variables, then the state of the input is represented by the vector \(\sigma=\sum_{i=1}^ne_i\otimes\sigma_i\) where \(e_i\) is the \(i^{th}\) canonical basis vector of \(\mathbb{Z}^n\). In other words, \(\sigma=\begin{pmatrix}\sigma_1&\cdots&\sigma_n\end{pmatrix}^T\in\{0,1\}^{M}\) where \(M=\sum_{j=1}^nm_j\) is formed from concatenating the one-hot encodings of each input variable. Let \(\mathcal{S}\) denote the set of valid \(\sigma\).

Assume the output variable \(y\) takes on one of \(m\) values, i.e. \(y\in\{1,\ldots,m\}\), then the probability distribution \(p:\mathcal{S}\rightarrow [0,1]\) is defined by

\[p(y=j~|~\sigma) = {e^{h_j(\sigma)} \over \sum_{i=1}^{m} e^{h_i(\sigma)}}\]

where \(h_i(\sigma)\) is the negative energy of the \(i^{th}\) state of \(y\) when the input state is \(\sigma\). \(p(y=j~|~\sigma)\) is the probability according to the Boltzmann distribution that \(y\) is in state \(j\) given that the input is in the state represented by \(\sigma\).

Importantly, \(h:\mathcal{S}\rightarrow\mathbb{R}^m\) maps \(\sigma\) to the negative energies of states of \(y\) in an interpretable manner:

\[h(\sigma) = \sum_{k=1}^KW_k\sigma^k.\]

The primary objective of FEM is to determine the model parameters that make up the matrices \(W_k\). \(\sigma^k\) is a vector of distinct powers of \(\sigma\) components.

The shapes of \(W_k\) and \(\sigma^k\) are \(m\times p_k\) and \(p_k\times1\), respectively, where \(p_k=\sum_{A\subseteq\{1,\ldots,n\}, |A|=k}\prod_{j\in A}m_j\). The number of terms in the sum defining \(p_k\) is \({n \choose k}\), the number of ways of choosing \(k\) out of the \(n\) input variables. The products in the formula for \(p_k\) reflect the fact that input variable \(x_j\) can take \(m_j\) states. Note that if all \(m_j=m\), then \(p_k={n\choose k}m^k\), the number ways of choosing \(k\) input variables each of which may be in one of \(m\) states.

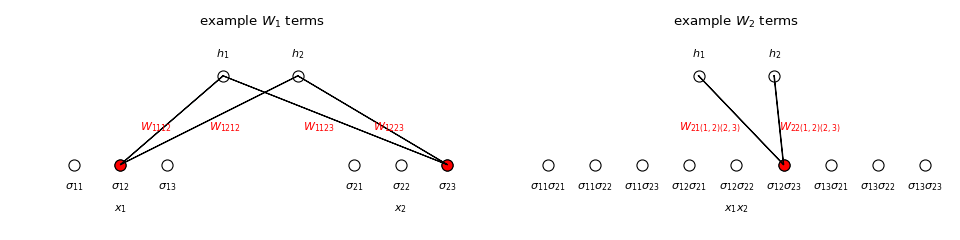
For example, if \(n=2\) and \(m_1=m_2=3\), then

\[\sigma^1 = \begin{pmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} & \sigma_{21} & \sigma_{22} & \sigma_{23} \end{pmatrix}^T,\]

which agrees with the definition of \(\sigma\) above, and

\[\sigma^2 = \begin{pmatrix} \sigma_{11}\sigma_{21} & \sigma_{11}\sigma_{22} & \sigma_{11}\sigma_{23} & \sigma_{12}\sigma_{21} & \sigma_{12}\sigma_{22} & \sigma_{12}\sigma_{23} & \sigma_{13}\sigma_{21} & \sigma_{13}\sigma_{22} & \sigma_{13}\sigma_{23} \end{pmatrix}^T.\]

Note that we exclude powers of the form \(\sigma_{ij_1}\sigma_{ij_2}\) with \(j_1\neq j_2\) since they are guaranteed to be 0. On the other hand, we exclude powers of the form \(\sigma_{ij}^k\) for \(k>1\) since they are guaranteed to be 1 as long as \(\sigma_{ij}=1\) and therefore would be redundant to the linear terms in \(h.\) For those reasons, \(\sigma^k\) for \(k>2\) is empty in the above example, and generally the greatest degree of \(h\) must satisfy \(K\leq n\), though this is hardly as restrictive as are computing abilities in real applications.

We say that \(h\) is interpretable because the effect of interactions between the input variables on the output variable is evident from the parameters \(W_k\). Consider the explicit formula for \(h\) for the example above with \(m=2\):

\[\begin{split}\begin{pmatrix} h_1(\sigma) \\ h_2(\sigma) \end{pmatrix} = \underbrace{\begin{pmatrix} W_{111} & W_{112} \\ W_{121} & W_{122} \end{pmatrix}}_{W_1} \begin{pmatrix} \sigma_{11} \\ \sigma_{12} \\ \sigma_{13} \\ \sigma_{21} \\ \sigma_{22} \\ \sigma_{23}\end{pmatrix} + \underbrace{\begin{pmatrix} W_{21(1,2)} \\ W_{22(1,2)} \end{pmatrix}}_{W_2}\begin{pmatrix} \sigma_{11}\sigma_{21} \\ \sigma_{11}\sigma_{22} \\ \sigma_{11}\sigma_{23} \\ \sigma_{12}\sigma_{21} \\ \sigma_{12}\sigma_{22} \\ \sigma_{12}\sigma_{23} \\ \sigma_{13}\sigma_{21} \\ \sigma_{13}\sigma_{22} \\ \sigma_{13}\sigma_{23} \end{pmatrix}.\end{split}\]

We’ve written \(W_1\) as a block matrix with \(1\times m_j\) row vector blocks \(W_{1ij}=\begin{pmatrix}W_{1ij1}&\cdots&W_{1ijm_j}\end{pmatrix}\) that describe the effect of \(x_j\) on \(y_i\). In particular, recalling that the probability of \(y=i\) given a input state \(\sigma\) is the \(i^{th}\) component of

\[\begin{split}p(y~|~\sigma) = {1 \over e^{h_1(\sigma)}+e^{h_2(\sigma)}} \begin{pmatrix} e^{h_1(\sigma)} \\ e^{h_2(\sigma)} \end{pmatrix}\end{split}\]

we see that \(h_i(\sigma)\) and hence the probability of \(y=i\) increases as \(W_{1ijs}\) increases when \(x_j=s\). In general, \(W_k\) can be written as \(n\) rows each with \({n \choose k}\) blocks \(W_{ki\lambda}\) of shape \(1\times\prod_{j\in\lambda}m_j\) where \(\lambda=(j_1,\ldots,j_k)\), which represent the effect that variables \(x_{j_1},\ldots,x_{j_k}\) collectively have on \(y_i\). That is \(h_i(\sigma)\) and hence the probability of \(y=i\) increases as \(W_{ki\lambda s}\) increases when \(x_{j_1}=s_1,\ldots,x_{j_k}=s_k\), where \(\lambda=(j_1,\ldots,j_k)\) and \(s=(s_1,\ldots,s_k)\).

(Source code, png, hires.png, pdf)

Method

Suppose we make \(\ell\) observations of the variables \(x_i, y\). We may arrange the one-hot encodings of these observations into matrices. Let \(\Sigma_{xk}\), \(k=1,\ldots,K\), be the matrix whose \(j^{th}\) column is the \(k^{th}\) power of the one-hot encoding of the \(j^{th}\) input observation \(\sigma_j^k\). Similarly, let \(\Sigma_y\) be the matrix whose \(j^{th}\) column is the one-hot encoding of the \(j^{th}\) output observation.

We summarize the probability of \(y=i\) given input observation \(\sigma_j\) in the matrix \(P(\Sigma_y~|~W)\) with elements

\[P_{ij} = {e^{H_{ij}} \over \sum_{i=1}^m e^{H_{ij}}},\]

where \(H_{ij}\) are the elements of the the matrix \(H = W\Sigma_x\) with

\[\begin{split}W = \begin{pmatrix} W_1 & \cdots & W_K \end{pmatrix}\hspace{5mm}\text{and}\hspace{5mm}\Sigma_x = \begin{pmatrix} \Sigma_{x1} \\ \vdots \\ \Sigma_{xK} \end{pmatrix}.\end{split}\]

\(\Sigma_x\) and \(\Sigma_y\) are computed solely from the data. We can adjust a guess at \(W\) by comparing the corresponding \(H\) and \(P(\Sigma_y~|~W)\), computed using the formulas above, to \(\Sigma_y\). That is, after modifying \(H\) to reduce the difference \(\Sigma_y-P(\Sigma_y~|~W)\) we can solve the formula \(H=W\Sigma_x\) for the model parameters \(W\). This is the motivation for the following method:

Initialize \(W^{(1)}=0\)

Repeat for \(k=1,2,\ldots\) until convergence:

\(H^{(k)} = W^{(k)}\Sigma_x\)

\(P_{ij}^{(k)} = {e^{H^{(k)}_{ij}} \over \sum_{i=1}^m e^{H^{(k)}_{ij}}}\)

\(H^{(k+1)} = H^{(k)}+\Sigma_y-P^{(k)}\)

Solve \(W^{(k+1)}\Sigma_x = H^{(k+1)}\) for \(W^{(k+1)}\)

The shapes of all matrices mentioned in this section are listed in the following table:

matrix	shape
\(\Sigma_x\)	\(\sum_{k=1}^np_k\times\ell\)
\(\Sigma_{xk}\)	\(p_k\times\ell\)
\(\Sigma_y\)	\(m\times\ell\)
\(P(\Sigma_y~|~W)\)	\(m\times\ell\)
\(H\)	\(m\times\ell\)
\(W\)	\(m\times\sum_{k=1}^np_k\)
\(W_k\)	\(m\times p_k\)

where \(p_k=\sum_{A\subseteq\{1,\ldots,n\}, |A|=k}\prod_{j\in A}m_j\).